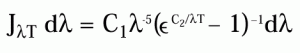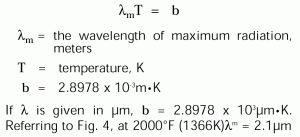Calibração infravermelho, todos os corpos emitem ao seu redor energia que é proporcional à sua temperatura absoluta. Ainda que a radiação emitida por um corpo inclua todos os comprimentos de onda, a faixa significativa para medição do sinal está aproximadamente entre 0,3µm e 20µm. Entre 0,4µm e 0,7µm está o espectro visível. A radiação com comprimento de onda maior que 0,7µm encontra-se na região do infravermelho, invisível ao olho nu.
Calibração Infravermelho, base teórica para medição de radiação
– Radiação do Corpo Negro
A energia térmica irradiada por um objeto é expressa em relação à energia irradiada por um corpo negro ideal na mesma temperatura. Um corpo negro absorve toda a radiação que recebe e emite mais radiação térmica de todos os comprimentos de onda que qualquer outro corpo com mesma área e temperatura.
Embora o corpo negro ideal seja teórico e inexistente, fontes de radiação especialmente construídas em laboratórios atingem 98% ou mais de eficiência, quando comparadas com o corpo negro ideal. Algumas fontes chegaram a atingir 99,98% de eficiência. A abordagem mais comum para a simulação de um corpo negro é a utilização de uma cavidade esférica com um pequeno furo na superfície, ou um tubo fechado com comprimento maior que seu diâmetro. As paredes opacas da esfera ou do tubo são mantidas a uma temperatura uniforme.
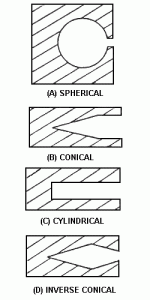
Figura 1
Conforme mostrado na figura 1 à direita, todos esses formatos causam a reflexão múltipla da radiação que entra por sua abertura. Assim, ainda que as paredes da esfera ou do tubo sejam ligeiramente reflexivas, eventualmente toda a energia será absorvida após muitas reflexões. Ou seja, à temperatura ambiente a abertura na esfera ou tubo aparenta ser totalmente negra para a parte visível do espectro, e também é uma boa aproximação para o restante do espectro. Para qualquer temperatura a abertura irradia energia em uma taxa praticamente igual à de um corpo negro de mesmo tamanho e temperatura. A figura 3b ilustra um forno comercial de referência secundária, baseado em uma pequena abertura em uma cavidade esférica uniformemente aquecida.
A figura2 ilustra um forno de referência secundário comercial baseado em uma pequena abertura em uma cavidade esférica uniformemente aquecida.
Outra configuração usada para uma fonte de corpo negro é uma cunha profunda, onde a cavidade subentende apenas um pequeno ângulo. Múltiplas reflexões dos lados da cunha fazem com que pareça preto. A importância real da cunha é conceitual. A rugosidade superficial de um objeto pode ser visualizada como uma multiplicidade de pequenas cunhas, como em uma superfície usinada ou fundição. Se a superfície for muito áspera, as cunhas são profundas e o objeto terá propriedades radiantes que são mais próximas às de um corpo negro do que se a superfície fosse lisa.
Lei de Stefan-Boltzman
A taxa pela qual um corpo negro irradia energia é dada pela Lei de Stefan-Boltzmann:
Esta equação pressupõe que o corpo que recebe a radiação está na temperatura do zero absoluto. Na prática, o corpo receptor está em uma temperatura TR e emite radiação para o corpo negro a uma taxa.
por unidade de área do receptor. Logo, a energia total recebida é:
onde K é uma constante, considerando-se as áreas do corpo negro, do receptor, e a distância entre eles.
Essas equações fornecem a radiação para todos os comprimentos de onda do espectro. Nos casos onde o objeto receptor (o detector em um termômetro por radiação, por exemplo) responde de forma significativa à parcela do espectro de ondas mais curtas, as Leis de Wien-Planck e Wien são mais práticas.
Lei de Wien-Planck
A Lei de Wien-Planck expressa a radiação emitida por unidade de área de um corpo negro em função do comprimento de onda, l, e da temperatura, T.
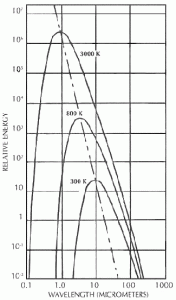
Foram plotados no gráfico da Figura 4 os resultados para várias temperaturas.
C1, a primeira constante de radiação = 3.7418 x 10-16 watts/m2
C2, a segunda constante de radiação = 1.43879 x 102 m • K
Wien’s Law
Se l T é menor que 0,003 m•K (3000 nm.K), os resultados para esta e a equação anterior divergem em menos de 1%. Para um comprimento de onda de 0,65 mm esta condição é válida para temperaturas menores que 4600K. Portanto a Lei de Wien tem sido utilizada com grande precisão na área de pirometria óptica.
Lei do Deslocamento de Wien
Pode ser observado na Fig. 4 que um aumento na temperatura, além de aumentar a radiação por unidade de área, reduz o comprimento de onda onde a radiação é máxima.
O valor do comprimento de onda de máxima radiação por unidade de área é dado pela Lei do Deslocamento de Wien.
Fig. 3 Intensidade da Radiação como Função do Comprimento de Onda e da Temperatura (Lei de Planck)
Geometria de Calibração
Todos os pirômetros infravermelhos, especialmente aqueles medindo comprimentos de onda longos, têm um “tamanho de efeito de fonte” (SSE), o que significa que parte de sua sensibilidade está fora do diâmetro do ponto especificado, causado por efeitos indesejados, inevitáveis como difração ou múltiplas reflexões. a lente e entre a lente e o detector.
Se calibrarmos para uma fonte com o diâmetro exato do ponto, qualquer um medindo grandes áreas receberia leituras tremendamente altas. Por outro lado, calibrar para uma fonte de radiação de área muito grande resultaria em uma leitura muito baixa para aqueles que medem um objeto no diâmetro do ponto.
As regras oficiais de calibração da VDI / VDE 3511 Parte 4.4 definem o “diâmetro de calibração” como um compromisso prático entre essas duas posições extremas.
Todos os pirômetros LumaSense são calibrados de acordo com essas regras.
Clique na informação técnica sobre geometria da calibração infravermelho
Clique em corpo negro de calibração de temperatura
Clique e conheça alternativas de pirômetros para a sua necessidade
Clique e saiba mais sobre câmeras termográficas
Calibração Infravermelho com corpo negro é na PerCon
Calibração infravermelho com corpo negro pode ser encontrado na PerCon Tecnologia sediada na Rua Dias da Cruz 188 – Sub solo – Méier (percon@acessopercon.com.br) / Fone : 21-2596-8369